Правильний шестикутник
| Правильний шестикутник | |
|---|---|

| |
| Тип | Правильний мгногокутник |
| Властивості | Опуклий, рівносторонній, ізогональний (вершинно-транзитивний), ізотоксальний (реберно-транзитивний), конциклічний (вписаний в коло), тангенціальний (описаний навколо кола) |
| Елементи | 6 ребер 6 вершин |
| Вершинна фігура | Відрізок довжиною |
| Позначення | |
| Символ Шлефлі | {6} (повна симетрія) t{3} (зрізаний трикутник) |
| Діаграма Коксетера-Динкіна |
|
| Група симетрії | D6, порядок 12 (Діедрична група) |
| Двоїстий | Самодвоїстий |
Правильний шестикутник (гексагон від грец. ἕξ, hex — шість та грец. γωνία, gonía — кут) — шестикутник, у якого всі сторони і кути рівні.
Також, правильний шестикутник — геометрична фігура, правильний многокутник з шістьма сторонами.
Правильний шестикутник можна отримати , застосовуючи операцію зрізання вершини до рівностороннього трикутника. Такий шестикутник має символ Шлефлі t{3}.
Правильний шестикутник може виступати гранями для шестикутної призми та антипризми, для п'яти напівправильних багатогранників Архімеда, а також для багатогранників Голдберга[en] та багатогранників Ватермана[en].
Правильний шестикутник має шість ліній дзеркальної симетрії, і обертову симетрію 6-го порядку (у 60°, 120°, 180°, 240° та 300°).
Оскільки сума внутрішніх кутів довільного опуклого шестикутника становить 720°, то кожен внутрішній кут правильного шестикутника дорівнює 120°.

Нехай — сторона правильного шестикутника,
R — радіус описаного кола,
r — радіус вписаного кола.
Для правильного шестикутника справедливі наступні формули:
Сторона правильного шестикутника:
У правильному шестикутнику сторона дорівнює радіусу описаного навколо нього кола.
Радіус вписаного кола правильного шестикутника (дорівнює апотемі правильного шестикутника) — дотикається до всіх його ребер:
Радіус описаного кола правильного шестикутника — проходить через всі його вершини:
Висота ‒ відстань між протилежними сторонами:
Із відношення радіусів описаного та вписаного кіл випливає, що відношення висоти до ширини правильного шестикутника дорівнює 1:1,1547005; тобто шестикутник із довгою діагоналлю 1 матиме відстань 0,8660254 між паралельними сторонами.
Площа правильного шестикутника:
|
|
де P — периметр правильного шестикутника: p — півпериметр; r = — радіус вписаного кола/ апотема. |

Внутрішнім кутом правильного шестикутника при даній вершині називається кут між двома його сторонами, що сходяться в цій вершині.
Сума внутрішніх кутів дорівнює радіан.
Зовнішнім кутом правильного шестикутника при цій вершині називається кут, суміжний внутрішньому куту шестикутника при цій вершині.
радіан.
Сума зовнішніх кутів (по одному при кожній вершині) дорівнює радіан.
Центральним кутом правильного шестикутника називається центральний кут його описаного кола, що спирається на його сторону. Величина центрального кута дорівнює:
радіан.

Правильний шестикутник має діагоналей:
- Шість діагоналей мають довжину
Коротка діагональ дорівнює висоті H шестикутника.
- Три діагоналі мають довжину
Довга діагональ правильного шестикутника вдвічі довша за його сторону.
З однієї вершини правильного шестикутника можна провести три діагоналі; вони ділять шестикутник на чотири трикутних частини, а внутрішній кут шестикутника ділять на чотири рівних частини.
Кут між будь-якими сусідніми діагоналями, що виходять з однієї вершини (включно зі сторонами, що виходять з цієї вершини):
Діагоналі правильного шестикутника перетинаються в 13 точках і ділять внутрішню область шестикутника на 24 частини (послідовності ![]() A006561 та
A006561 та ![]() A007678).
A007678).
Короткі діагоналі при перетині утворюють гексаграму. Довгі діагоналі перетинаються в одній точці — центрі правильного шестикутника.
Сума квадратів всіх сторін та всіх діагоналей правильного шестикутника, вписаного в коло радіуса R дорівнює 36R2 [1].
- Правильний шестикутник є рівносторонній і рівнокутний одночасно. Він є вписаним і описаним одночасно.
- Центри вписаного та описаного кіл збігаються та лежать в центрі правильного шестикутника. Також в центрі правильного шестикутника знаходиться його центр мас.
- Площа кільця, утвореного вписаним та описаним колом залежить тільки від довжини сторони:
- Радіус описаного кола правильного шестикутника дорівнює його стороні. Інші відомі багатогранники (політопи), які мають цю властивість, це Кубооктаедр (а також усі розширені[en] симплекси), тесеракт та 24-комірник. Завдяки цьому правильний шестикутник можна точно розкласти на 6 рівносторонніх трикутників.
- Правильний шестикутник може бути побудований за допомогою циркуля та лінійки без міток.

Гексаграма - У правильного шестикутника існує тільки одна зірчаста форма — гексаграма (шестикутна зірка, що утворена поєднанням двох правильних трикутників).
Правильний шестикутник і правильний п'ятикутник є єдиними багатокутниками з однією можливою зірчастою формою. Це також багатокутник із найбільшою кількістю сторін, який не має простої зірки, тобто зірки, що не утворена поєднанням інших багатокутників. Інші багатокутники, що не мають простих зірок (і зірок взагалі) — це трикутник і квадрат. Це також єдиний правильний багатокутник, який має лише складені (непрості) зірки.
Замощення площини правильними шестикутниками - Правильний шестикутник є одним із трьох правильних багатокутників, якими можна замостити площину без проміжків та накладень; два інші — рівносторонній трикутник і квадрат. Шестикутний паркет має 3 шестикутники при вершині. Також використовується в інших однорідних та напівправильних паркетах.
- Правильний шестикутник є перестановковим многогранником[en] порядку 3.
- Правильний шестикутник, у якого відстань між протилежними сторонами дорівнює 1 є універсальним покриттям:
Лема Пала: будь-яку множину діаметром 1 можна покрити правильним шестикутником, у якого відстань між протилежними сторонами дорівнює 1 (шестикутник з довжиною сторони )[2][3][4][5].
Лему довів угорський математик Д. Пал[en] 1929 року.

Нехай точка Р — довільна точка всередині правильного шестикутника. З неї на сторони опущені перпендикуляри.
— апотема правильного шестикутника (перпендикуляр, опущений з його центра на будь-яку з його сторін).
Тоді виконується така рівність:
Названа іменем італійського математика Вінченцо Вівіані[6].[1]

Навколо правильного шестикутника ABCDEF описано коло. Точка Р лежить на описаному колі між вершинами В і С. Тоді:
Нехай — відстані від точки P на описаному колі правильного шестикутника до його вершин. Тоді:[7]
Сума квадратів відстаней від вершин правильного шестикутника до будь-якої точки на його описаному колі дорівнює 12R2[1]
Сума квадратів відстаней від середин сторін правильного шестикутника до будь-якої точки на його описаному колі дорівнює 12R2 − 3/2a2,[1]
де a — довжина сторони правильного шестикутника.
Навколо правильного шестикутника описано коло радіусом R.
Точка Р знаходиться в площині шестикутника. ОР = L — відстань від точки Р до центра шестикутника (центра описаного кола). (i = 1, 2…5) — відстані від точки Р до вершин шестикутника.
Тоді виконуються наступні рівності:[7]

Правильний шестикутник має діедричну групу симетрії D6 (або Dih6), порядку 12.
Вона складається з 6 обертових симетрій (у 60°, 120°, 180°, 240° та 300°) і 6 осьових симетрій.
Правильний шестикутник має 6 ліній дзеркальної симетрії: 3 осі симетрії, що проходять через дві протилежні вершини, та 3 осі симетрії, що проходять через середини протилежних сторін. Є центр симетрії.

Група симетрії D6 містить 16 підгруп. Це 8 підгруп включно з ізоморфізмами: власне D6 , 2 діедричні (D3, D2), 4 циклічні (Z6, Z3, Z2, Z1), та тривіальна (e).
Ці типи симетрії у правильному шестикутнику можна побачити у вигляді 9 різних симетрій. Джон Конвей позначав їх за допомогою літери і порядку групи.[8]
Повна симетрія правильної форми — r12 і відсутність симетрії — a1.
p6, ізогональний шестикутник, побудований з трьома відзеркаленнями, для неправильних форм може чергувати довгі та короткі ребра.
d6, ізотоксальний шестикутник, побудований з рівними довжинами ребер, але вершини чергуються з двома різними внутрішніми кутами (для неправильних форм).
Ці дві форми є двоїстими одна до одної та мають половинний порядок симетрії правильного шестикутника.
Форми i4 являють собою правильні шестикутники, сплющені або витягнуті вздовж одного напрямку симетрії.
| Приклади шестикутників згідно симетрії | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Його можна розглядати як подовжений ромб, тоді як d2 і p2 можна розглядати як горизонтально та вертикально подовжені дельтоїди. g2 шестикутники, протилежні сторони яких паралельні, також називають шестикутними паралелогонами.
Кожна підгрупа симетрії допускає один або більше ступенів вільності для неправильних форм. Лише підгрупа g6 не має ступенів вільності, але її можна розглядати як орієнтований граф. Шестикутники з симетрією g2, i4, та r12, як паралелогони можуть замостити евклідову площину шляхом копіювання. Інші форми шестикутника замощують площину в різних орієнтаціях.
Правильний шестикутник можна побудувати за допомогою циркуля і лінійки, оскільки число є добутком двійки на просте число Ферма, що згідно з теоремою Гаусса — Ванцеля є достатньою умовою для можливості його побудови за допомогою циркуля і лінійки.

- Будуємо коло вибраного радіуса та проводимо його діаметр.
- З протилежних кінців цього діаметра описуємо дуги циркулем, розхил якого рівний радіусу кола.
- Точки перетину цих дуг з колом, а також два кінці діаметра кола є вершинами правильного шестикутника.

Дано відрізок АВ, що дорівнює стороні правильного шестикутника.
З кінців відрізка радіусом, рівним АВ проводимо дві дуги до їх перетину в точці М.
Із точки М цим же радіусом проводимо коло.
Починаючи з точки В радіусом АВ відмічаємо на цьому колі ще чотири вершини шуканого шестикутника.

Наближення до правильного шестикутника, яке часто є достатнім для практичних цілей, отримують, якщо шестикутник побудовано з приблизно рівносторонніх трикутників, які мають співвідношення висоти до основи 7:8 (7 одиниць довжини в висоту та 8 одиниць довжини основи). Кути цього трикутника майже дорівнюють 60о.
Це наближення застосовується, коли допускається похибка трохи менше 1%. Наприклад, при розмітці клумб, міських площ, ігрових полів та ін.
Точки Pi (x|y) пронумеровані нижче відповідно до цифр годинника, центр (0|0):
- Координати вершин шестикутника в горизонтальному положенні:
- P1 (4|7), P3 (8|0), P5 (4|−7), P7 (−4|−7), P9 (−8|0), P11 (−4|7)
- Координати вершин шестикутника в вертикальному положенні:
- P2 (7|4), P4 (7|−4), P6 (0|−8), P8 (−7|−4), P10 (−7|4), P12 (0|8)
Краще наближення можна отримати, замінивши числа 4, 7 і 8 у наведених вище координатах на 15, 26 і 30 відповідно. Інші можливі трійки: (56, 97, 112) або (209, 362, 418).
Правильний шестикутник можна скласти методами оригамі, використовуючи дві смуги паперу однакової ширини.[5]

| Проекція 6-куба | Розбиття на 3 ромби | Розбиття на 12 ромбів | |
|---|---|---|---|

|

|

|

|
Гарольд Коксетер стверджує, що кожен зоногон (2m-кутник, протилежні сторони якого паралельні й мають однакову довжину) можна розрізати на
Зокрема, це справедливо для будь-якого правильного багатокутника з парною кількістю сторін, у цьому випадку всі паралелограми є ромбами.
Це розбиття правильного шестикутника базується на багатокутнику Петрі[en] проекції куба, з 3 із 6 квадратних граней.
Правильний шестикутник має символ Шлефлі {6}. Правильний шестикутник є частиною правильного шестикутного паркету {6,3} з трьома шестикутними гранями навколо кожної вершини.
Правильний шестикутник також можна утворити, застосувавши операцію зрізання вершини до рівностороннього трикутника. Такий шестикутник має символ Шлефлі t{3}. Оскільки ця форма має два типи (кольорів) сторін, то її симетрія лише D3.
Зрізаний шестикутник, t{6}, є дванадцятикутником, в якого чергуються два типи (кольорів) сторін.
Альтернований[en] шестикутник, h{6}, є правильним трикутником {3}.
Правильний шестикутник має зірчасту форму, гексаграму.
Правильний шестикутник можна розбити на шість рівносторонніх трикутників, з вершинами в центрі шестикутника. Цей візерунок повторюється в межах правильного трикутного паркету.
Правильний шестикутник можна розширити до правильного дванадцятикутника, додавши навколо нього квадрати та рівносторонні трикутники, що чергуються. Цей візерунок повторюється в ромботришестикутному паркеті[en].

|

|

|

|

|

|

|
| Правильний шестикутник
{6} |
Зрізаний правильний трикутник
t{3} = {6} |
Гіперзрізаний трикутник | Зірчаста форма | Зрізаний правильний шестикутник
t{6} = {12} |
Альтернований правильний шестикутник
h{6} = {3} |
Розширення правильного {6} в {12} |
|---|
Серед правильних багатогранників Платона не існує таких, що мають шестикутні грані. Однак правильний шестикутник можна отримати як переріз правильних багатогранників площиною, або при їх ортогональних проєкціях.
Площина, що перетинає правильний багатогранник по шестикутному перерізу, проходить через центр багатогранника та середини його протилежних паралельних ребер, та розділяє його на дві рівні частини. Площина шестикутного перерізу в кубі та додекаедрі перпендикулярна до їх діагоналі.[10][11][12]
| Шестикутники у багатогранниках Платона | ||||||
|---|---|---|---|---|---|---|
| Переріз октаедра площиною | Переріз куба площиною | Переріз додекаедра площиною | Проєкція октаедра, центрована по грані | Проєкція куба, центрована по вершині | Проєкція ікосаедра, центрована по грані | |

|

|

|

|

|

|
|
Багатогранники Архімеда: зрізаний тетраедр, зрізаний октаедр, зрізаний ікосаедр, зрізаний кубооктаедр та зрізаний ікосододекаедр, мають в складі своїх граней правильний шестикутник. Ці шестикутники можна вважати зрізаними трикутниками, а тому багатогранники мають діаграми Кокстера у вигляді ![]()
![]()
![]()
![]()
![]() та
та ![]()
![]()
![]()
![]()
![]() .
.
| Шестикутники в багатогранниках Архімеда | ||||
|---|---|---|---|---|
| Тетраедрична симетрія | Октаедрична симетрія | Ікосаедрична симетрія | ||
 Зрізаний тетраедр |
 Зрізаний октаедр |
 Зрізаний кубооктаедр |
 Зрізаний ікосаедр |
 Зрізаний ікосододекаедр |
Існують інші багатогранники даних симетрій з деформованими (розтягнутими або сплощеними) шестикутниками, зокрема багатогранник Голдберга[en] G(2,0):
| Шестикутник в багатогранниках Голдберга | ||
|---|---|---|
| Тетраедрична симетрія | Октаедрична симетрія | Ікосаедрична симетрія |
 Тетраедр з фаскою[en] |
 Куб з фаскою |
 Додекаедр з фаскою |
Існує 9 многогранників Джонсона, гранями яких є правильний шестикутник:
| Шестикутник в багатогранниках Джонсона | |||
|---|---|---|---|
 Трисхилий купол |
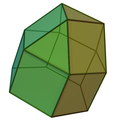 Подовжений трисхилий купол |
 Скручений подовжений трисхилий купол | |
 Нарощена шестикутна призма |
 Двічі протилежно нарощена шестикутна призма |
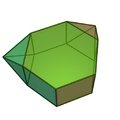 Двічі косо нарощена шестикутна призма |
 Тричі нарощена шестикутна призма |
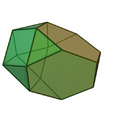 Нарощений зрізаний тетраедр |
 Сплощена трикутна клиноротонда |
 Зрізаний тріакістетраедр | |
Призматоїди з шестикутними гранями:
| Шестикутники в призматоїдах | |||||
|---|---|---|---|---|---|
 Шестикутна призма Шестикутна призма
|
 Шестикутна антипризма Шестикутна антипризма
|
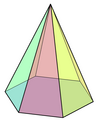 Шестикутна піраміда Шестикутна піраміда
|
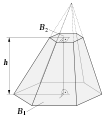 Зрізана шестикутна піраміда Зрізана шестикутна піраміда
|
Інші | |
 Шестикутна зрізана біпіраміда Шестикутна зрізана біпіраміда
|
 Зрізаний шестикутний трапецоедр Зрізаний шестикутний трапецоедр
| ||||
Паркети з правильними шестикутниками
| Правильні шестикутники в паркетах | |||
|---|---|---|---|
| Regular | 1-uniform | ||
| Шестикутний паркет{6,3}
|
Тришестикутний паркетr{6,3}
|
Ромботришестикутний паркет
rr{6,3}
|
Зрізаний тришестикутний паркет
tr{6,3}
|

|

|

|

|
| 2-однорідні паркети | |||

|

|

|

|
- Бджолині стільники наочно показують розбиття площини на правильні шестикутники.
- Деякі складні молекули вуглецю (наприклад, графіт) мають гексагональну кристалічну ґратку.
- Шестикутник Сатурна — атмосферне явище поблизу північного полюса планети Сатурн.
- Сортамент сортового прокату "шестигранник" (з якого виготовляються гайки, болти), шестигранні ключі, а також багато видів олівців у поперечному перерізі мають форму правильного шестикутника.
- Контур Франції нагадує правильний шестикутник, тому ця фігура — символ країни. Вислів «гексагон» у французькій мові широко вживається як перифраз назви «Франція». Форма шестикутника використовується також на французьких монетах євро. Щоправда, порівняння Франції з шестикутником відносно недавнє[13].
- Гексагональні шахи — різновид гри в шахи на шестикутній дошці з шестикутними (гексагональними) полями.
- Головне дзеркало космічного телескопа Джеймса Вебба складається з 18 шестикутників по 1,3 м кожен, які можна регулювати з високою точністю.
-
Графен - одна з модифікацій вуглецю
-
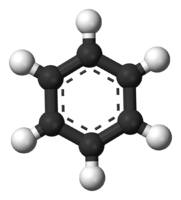
Бензен — найпростіша ароматична сполука шестикутної форми.
-
Кристалічна структура молекулярного шестикутника, що складається з шестикутних ароматичних кілець.
-
Шестикутна гайка з гвинтом з шестигранним шліцем
-
Інбусові ключі різних розмірів
-
Гігантький гексагон Сатурна
-
Вид на Форт Джефферсон у національному парку Драй-Тортугас[en]
-
Шестикутні панелі з термопластику в проєкті «Едем»
-
Шестикутне вікно в домі Мустонена (Йоенсуу)
- Правильний багатокутник
- Шестикутне число
- Шестикутна зірка (гексаграма)
- Теорема Гауса-Ванцеля
- Щільне пакування рівних сфер
- Флексагон
- Магічні шестикутники[en]
- ↑ а б в г Johnson, Roger A. (2007 (orig. 1929)). Advanced Euclidean Geometry (PDF) (англ.) . Dover Publ. с. 319:стор.72-73.
- ↑ Peter, Brass (2005), A lower bound for lebesgue`s universal cover problem (PDF), International Journal of computational Geometry & Applications
- ↑ Gábor Fejes, Tóth; Kuperberg, Włodzimierz (2022), Four classic problems (PDF), Birkhäuser
- ↑ Хадвигер, Гуго; Дебруннер, Ганс (H. Hadwiger, H. Debrunner). (1965), Комбинаторная геометрия плоскости. (Kombinatorische geometrie in der ebene) (ru Переклад з німецької) , «Наука»: Главная редакция физико-математической литературы
- ↑ а б Wells, David (1991), The Penguin dictionary of curious and interesting geometry (англ.) , London: Penguin, с. 287:191-192
- ↑ Abboud, Elias (2010). On Viviani’s Theorem and its Extensions. College Mathematics Journal. 43 (3): 16. arXiv:0903.0753v3.
- ↑ а б Meskhishvili, Mamuka (2020). Cyclic Averages of Regular Polygons and Platonic Solids. Communications in Mathematics and Applications. 11: 335—355. arXiv:2010.12340. doi:10.26713/cma.v11i3.1420.
- ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275—278)
- ↑ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
- ↑ ,Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, 1999. p. 170 ISBN 978-0486409146
- ↑ Cundy, H. and Rollett, A. "Hexagonal Section of a Cube." §3.15.1 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., p. 157, 1989. ISBN 978-0906212202
- ↑ Weisstein, Eric W. (1998), CRC Concise Encyclopedia of Mathematics (англ.) , CRC Press LLC, с. 1969, ISBN 0-8493-9640-9
- ↑ Nathaniel B. Smith, «The idea of the French Hexagon», dans French historical studies, vol. 6, no 2, 1969, p. 139–155 (ISSN 0016-1071).
- Weisstein, Eric W. Regular Hexagon(англ.) на сайті Wolfram MathWorld.
- Hexagon(англ.) на сайті Polytope Wiki.
- Hall of Hexagons
- Math Open Reference: Hexagon (6-gon)
- Math is Fun: Hexagon
- An Introduction to Hexagonal Geometry on Hexnet вебсайт, присвячений шестикутнику.
- Hexagons are the Bestagons на YouTube.

















































![Гексагональний кристал ганкситу[en], один із багатьох мінералів гексагональної кристалічної системи](http://upload.wikimedia.org/wikipedia/commons/thumb/4/4e/Hanksite.JPG/200px-Hanksite.JPG)





![Вид на Форт Джефферсон у національному парку Драй-Тортугас[en]](http://upload.wikimedia.org/wikipedia/commons/thumb/5/5f/Fort-Jefferson_Dry-Tortugas.jpg/200px-Fort-Jefferson_Dry-Tortugas.jpg)

